كيف يعلم علم الرياضيات؟
كيف يتعلم التلاميذ؟
كيف يتم توظيف الأفكار السابقة (الأعمال الموجهة)
- Dr. MAADADI Asma: asma maadadi
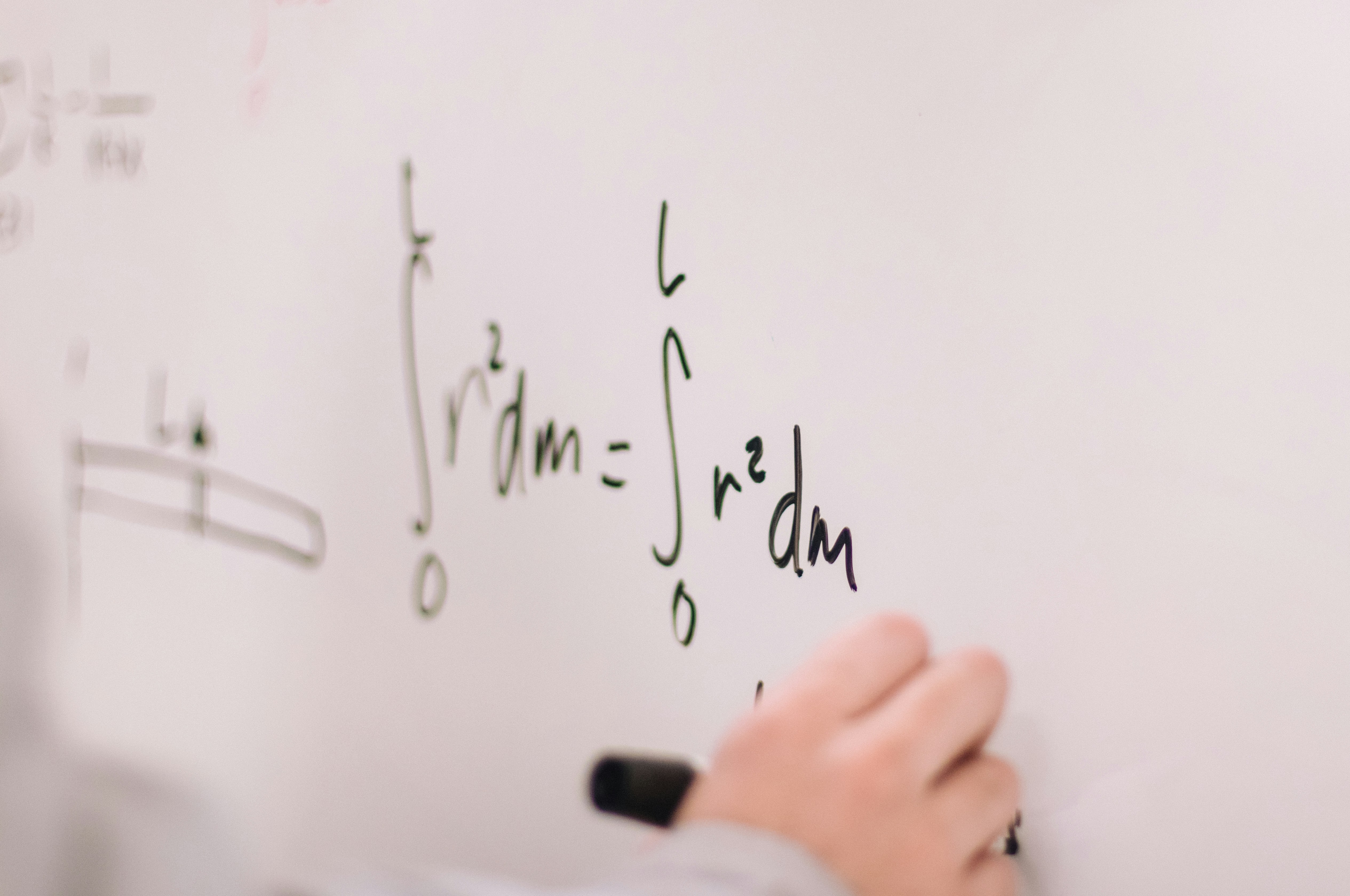
This course, intended for third-year undergraduate mathematics students,
introduces the fundamental concepts of measure theory and Lebesgue integration.
It extends the classical Riemann integral to a more general and powerful framework,
essential for modern analysis, probability theory, and functional analysis.
The module covers the construction of measures (in particular the Lebesgue measure),
the study of measurable functions, and the definition of the Lebesgue integral.
Special attention is given to the main convergence theorems
(Monotone Convergence, Fatou’s Lemma, Dominated Convergence),
which play a central role in analysis.
By the end of the course, students will understand the necessity of measure theory,
be familiar with the Lebesgue integral and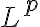 
spaces,
and be prepared for advanced studies in analysis and its applications.
- Dr.: fares bensaid
This course introduces the fundamental concepts and theorems needed for the qualitative study of ordinary differential equations (ODEs). It builds on prior knowledge in real analysis, linear algebra, and topology.
Main Topics Covered
-
First-Order Equations
-
Fundamental results
-
Local and global existence, uniqueness of solutions
-
Dependence on initial conditions
-
-
Higher-Order Equations and First-Order Systems
-
General theory of higher-order differential equations
-
Equivalence with systems of first-order equations
-
-
Linear Systems
-
Matrix exponential
-
Second-order systems
-
-
Introduction to Stability Concepts
-
Basic notions and principles related to the stability of solutions
-
In short, the course provides a comprehensive foundation in ordinary differential equations, combining theory (existence, uniqueness, stability) with methods for solving and analyzing both first-order and higher-order systems.
Evaluation
-
Final Exam: 60%
-
Continuous Assessment: 40%
- Teacher: Bilal Ghermoul