Les Travaux Pratiques Méthode Numérique sont destinés aux étudiants de deuxième Année Licence Electromécanique. Ils regroupent un certain nombre de méthodes étudiées dans les différents chapitres du cours de méthodes numériques.
L’objectif de ces TP est d’implémenter ou programmer sous MATLAB les différentes méthodes d'approximation.
- Enseignant: abdelaziz diaf
- Enseignant: ibtissem belgasmi
Connaitre les méthodes de calcul à la résistance des éléments des constructions et déterminer les variations de la forme et des dimensions (déformations) des éléments sous l’action des charges.
- Enseignant: asma talbi
La mesure joue un rôle de plus en plus important dans les domaines électriques et électroniques. On mesure avec pour but la vérification expérimentale d'un circuit, la modélisation, la mise au point ou le dépannage d'un montage, la certification d'un procédé ou d'un produit, dans le domaine industriel et la maintenance ou la réparation d'un dispositif électrique ou électronique. Dans le domaine électrique et électronique, on utilise plusieurs types d'appareils de mesure, tels que les voltmètres ( analogique et numérique) pour mesurer des tensions, les ampèremètres pour mesurer des intensités, les wattmètre pour mesurer des puissances et les ohmmètres pour mesurer des résistances etc...
- Enseignant: fateh slama
This summary covers the main numerical methods studied in the following chapters:
Chapter 1: Solving Nonlinear Equations f(X) = 0
1. Bisection Method: A method to find a root of an equation by dividing the search interval into two equal parts and selecting the interval containing the root.
2. Fixed-Point Method: A method to find a root of an equation by transforming the equation into an equivalent form ( X = g(X)) and iterating the function ( g ) from an initial guess ( X_0 ) until convergence to the root.
3. Newton-Raphson Method: A method to find a root of an equation using the tangent approximation of the function ( f ) at ( X0) and iterating toward the root.
Chapter 2: Polynomial Interpolation
1. Lagrange Method: A method to interpolate a function using a polynomial of degree ( n ) that passes through ( n+1 ) points.
2. Divided Differences Method (Newton's Polynomial): A method to interpolate a function using a polynomial of degree ( n ) that passes through ( n+1 ) points, with coefficients calculated using divided differences.
Chapter 3: Numerical Integration
1. Trapezoidal Rule: A method to compute the integral of a function by approximating the area under the curve using trapezoids between interval points.
2. Simpson's Rule: A method to compute the integral of a function by approximating the curve with a second-degree polynomial.
Chapter 4: Solving Differential Equations
1. Euler's Method: A method to solve ordinary differential equations by approximating the solution with straight-line segments.
2. Modified Euler's Method: A method to solve ordinary differential equations using an improved approximation of the average slope.
3. Runge-Kutta Method (2nd Order): A method to solve ordinary differential equations using a weighted average slope approximation.
4. Runge-Kutta Method (4th Order): A method to solve ordinary differential equations using a more accurate weighted average slope approximation with four steps.
Chapter 5: Direct Methods for Solving Systems of Linear Equations
1. Gaussian Elimination: A method to solve systems of linear equations by transforming the system into an upper triangular form using elementary row operations.
2. Gauss-Jordan Elimination: A method to solve systems of linear equations by transforming the system into reduced row echelon form using elementary row operations.
3. Tri-diagonal Matrices (Thomas Algorithm): A method to solve tridiagonal systems of linear equations using forward and backward substitution.
- Enseignant: mourad hamimid
- Enseignant: djamila zehar
- Enseignant: abderazak bennia
Cet enseignement vise à développer les compétences de l’étudiant, sur le plan personnel ou professionnel, dans le domaine de la communication et des techniques d’expression.
- Enseignant: idhir nezzari
- Enseignant: abdallah bengueddoudj
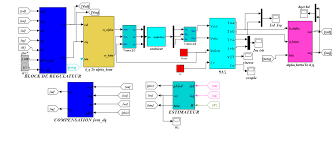
Savoir modéliser et appliquer les techniques de commandes étudiées sur des machines électriques. Vérifier le comportement dynamique des systèmes commandés (machines avec boucles de commande). Implémentation et calcul des régulateurs PID.
- Enseignant: badria amara
Tp
- Enseignant: asma ammarboudjellal
Ce manuel de travaux pratiques couvre l’ensemble des manipulations de la matière TP logique combinatoire et séquentielle dédié aux étudiants de la 2éme année licence électromécanique et électronique conformément au canevas harmonisé puis révisé en 2018.
Cette matière vient de consolider par la pratique, les connaissances acquises pendant le cours de la matière logique combinatoire et séquentielle, elle permettra à l’étudiant d’acquérir un savoir faire consistant pour bien assimiler les connaissances théoriques.
- Enseignant: toufik bekkouche